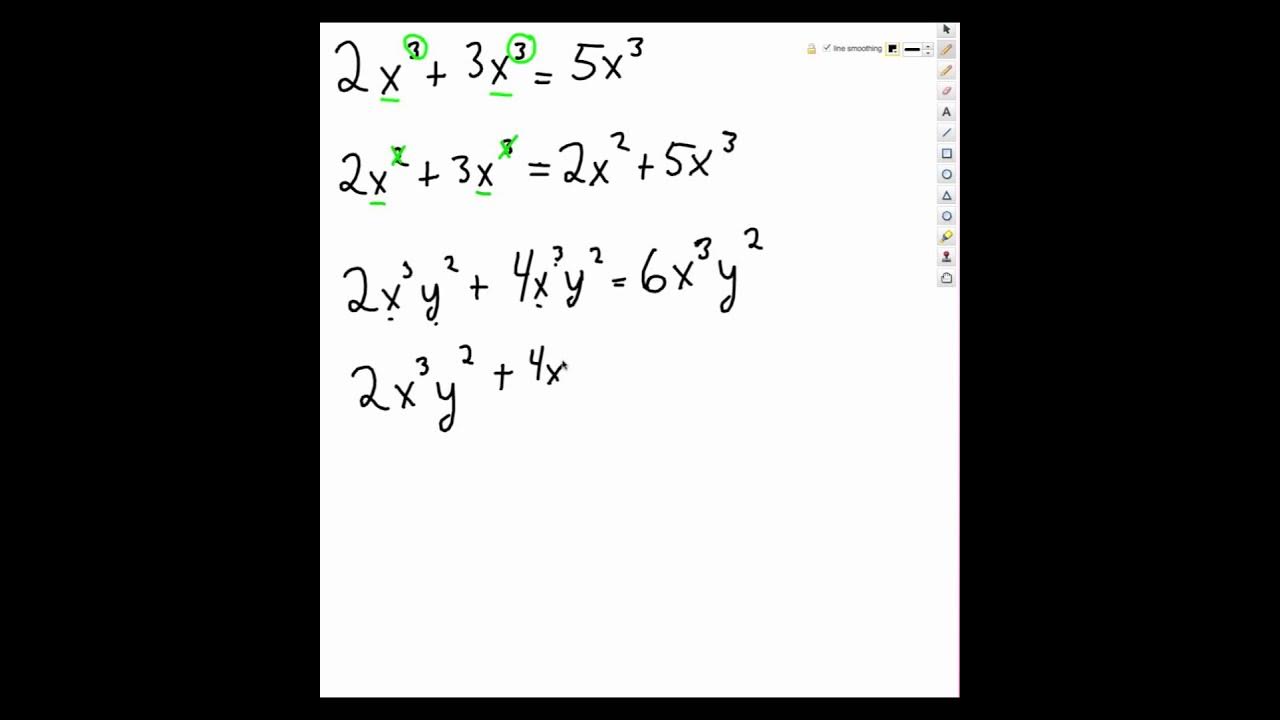
When adding terms with exponents, the base must be the same. If the bases are the same, add the exponents and keep the base.
For example, to add x2 + x2, we add the exponents to get x4. The base stays the same.
This rule is important because it allows us to simplify expressions and solve equations. For example, we can use this rule to simplify the expression (x2 + x2)2. First, we add the exponents to get x4. Then, we square x4 to get x8.
This rule also helps us to solve equations. For example, we can use this rule to solve the equation x2 + x2 = 16. First, we add the exponents to get x4 = 16. Then, we take the fourth root of both sides to get x = 2.
What Do I Do With Exponents When Adding
When adding terms with exponents, it is important to consider the following key aspects.
- Base: The base is the number that is being raised to the power of the exponent. When adding terms with exponents, the bases must be the same.
- Exponent: The exponent is the number that tells us how many times the base is multiplied by itself. When adding terms with exponents, we add the exponents.
- Simplify: Once we have added the exponents, we can simplify the expression by multiplying the coefficients and combining like terms.
- Equation: We can use the rule for adding exponents to solve equations that involve exponents.
- Variable: Exponents can be used to represent variables. This can be useful for simplifying expressions and solving equations.
- Power: Exponents can be used to represent powers. This can be useful for simplifying expressions and solving equations.
These key aspects are all important for understanding how to add terms with exponents. By understanding these aspects, we can simplify expressions, solve equations, and more.
Base
The base is a fundamental concept in working with exponents. It represents the number that is being multiplied by itself repeatedly. When adding terms with exponents, it is essential to ensure that the bases are the same. If the bases are different, the terms cannot be combined.
For example, consider the following expression: x2 + y2. In this expression, the bases are x and y. Since the bases are different, the terms cannot be combined. However, if we change the expression to x2 + x2, the bases are the same and the terms can be combined. The result is 2x2.
Understanding the concept of the base is crucial for adding terms with exponents. By ensuring that the bases are the same, we can simplify expressions and perform calculations more efficiently.
Exponent
The concept of exponents is closely connected to "what do I do with exponents when adding" because exponents dictate how terms are added. When adding terms with exponents, the bases must be the same. The exponent tells us how many times the base is multiplied by itself. By understanding the concept of exponents, we can simplify expressions and perform calculations more efficiently.
For example, consider the following expression: x2 + x2. In this expression, the base is x and the exponent is 2. This means that x is multiplied by itself twice. To add these terms, we add the exponents, which gives us x4. The result is x multiplied by itself four times.
Understanding the connection between exponents and adding terms with exponents is essential for simplifying expressions and solving equations. It allows us to perform calculations more efficiently and accurately.
Simplify
The step of simplifying an expression after adding exponents is an integral part of "what do I do with exponents when adding." This step involves multiplying the coefficients of the terms and combining like terms. By simplifying the expression, we obtain a more concise and manageable form that facilitates further calculations or analysis.
For instance, consider the expression x2 + x2. After adding the exponents, we get x4. However, the expression can be further simplified by multiplying the coefficients, which results in 2x4. This simplified form is more convenient for subsequent operations or interpretation.
The ability to simplify expressions is particularly important in solving equations involving exponents. By simplifying the expression, we can isolate the variable and determine its value more efficiently. Additionally, simplifying expressions is crucial for various applications in mathematics, science, and engineering, where complex expressions are often encountered.
Therefore, understanding how to simplify expressions after adding exponents is essential for effectively working with exponents. It enables us to simplify complex expressions, solve equations, and apply exponents in practical scenarios.
Equation
The connection between "Equation: We can use the rule for adding exponents to solve equations that involve exponents" and "what do I do with exponents when adding" lies in the practical application of the rule for adding exponents. When solving equations involving exponents, understanding how to add exponents is crucial for simplifying the equation and isolating the variable.
- Solving Linear Equations: Adding exponents is essential in solving linear equations that involve exponents. By adding the exponents of like terms, we can simplify the equation and isolate the variable to determine its value. This technique is widely used in algebra and other mathematical applications.
- Simplifying Exponential Equations: The rule for adding exponents allows us to simplify exponential equations by combining like terms. This simplification process enables us to solve the equation more efficiently and accurately. Simplifying exponential equations is crucial in various fields, including calculus, physics, and engineering.
- Inequalities with Exponents: Adding exponents is also useful in solving inequalities that involve exponents. By understanding how to add exponents, we can simplify the inequality, isolate the variable, and determine the range of possible values for the variable that satisfy the inequality.
- Applications in Real-Life Situations: The ability to solve equations involving exponents has practical applications in various fields, including exponential growth and decay models, radioactive decay, and population growth. Understanding how to add exponents is essential for accurately predicting and analyzing these real-life scenarios.
In conclusion, the connection between "Equation: We can use the rule for adding exponents to solve equations that involve exponents" and "what do I do with exponents when adding" lies in the practical application of exponent addition in solving equations and simplifying expressions. By understanding the rule for adding exponents, we can effectively solve equations involving exponents, simplify exponential expressions, and apply these concepts in various real-life situations.
Variable
The connection between "Variable: Exponents can be used to represent variables. This can be useful for simplifying expressions and solving equations." and "what do I do with exponents when adding" lies in the fundamental role of variables in algebraic expressions and equations. When exponents are used to represent variables, it allows for more compact and efficient representation, simplification, and manipulation of mathematical expressions.
One of the key benefits of using exponents to represent variables is the ability to simplify complex expressions. For instance, instead of writing out (x + y)(x + y)(x + y), we can use the exponential notation (x + y)3 to represent the same expression. This simplified notation makes it easier to perform calculations and identify patterns.
Furthermore, using exponents to represent variables is essential for solving equations. Consider the equation x2 - 5 = 0. Without using exponents, it would be difficult to find the value of x that satisfies this equation. However, by recognizing that x2 represents x multiplied by itself twice, we can rewrite the equation as (x)2 - 5 = 0. This allows us to take the square root of both sides of the equation, resulting in x = 5.
The understanding of how to work with exponents when adding, including the use of exponents to represent variables, is crucial in various fields of science, technology, engineering, and mathematics. It enables researchers, engineers, and mathematicians to simplify complex expressions, solve complex equations, and model real-world phenomena more accurately.
In summary, the connection between "Variable: Exponents can be used to represent variables. This can be useful for simplifying expressions and solving equations." and "what do I do with exponents when adding" lies in the power of exponents to simplify and manipulate algebraic expressions and equations. It is a fundamental concept that underpins many advanced mathematical operations and has practical applications in various fields.
Power
The connection between "Power: Exponents can be used to represent powers. This can be useful for simplifying expressions and solving equations." and "what do I do with exponents when adding" lies in the fundamental role of exponents in representing mathematical operations. Exponents allow us to simplify and manipulate expressions involving powers, which is essential for solving equations and performing various mathematical calculations.
- Simplifying Expressions:
Exponents can be used to simplify expressions by representing repeated multiplication. For instance, instead of writing 3 3 3 3 3, we can use the exponential notation 3^5 to represent the same value. This simplified notation makes it easier to perform calculations and identify patterns.
- Solving Equations:
Exponents are crucial for solving equations involving powers. Consider the equation x^2 - 9 = 0. Without using exponents, it would be difficult to find the value of x that satisfies this equation. However, by recognizing that x^2 represents x multiplied by itself twice, we can rewrite the equation as (x)^2 - 9 = 0. This allows us to take the square root of both sides of the equation, resulting in x = 3 or x = -3.
- Real-Life Applications:
The understanding of how to work with exponents when adding, including the use of exponents to represent powers, has practical applications in various fields. For example, in physics, exponents are used to represent powers of 10 in scientific notation, making it easier to express very large or very small numbers. In engineering, exponents are used to calculate powers of 2 in computer science and digital signal processing.
In summary, the connection between "Power: Exponents can be used to represent powers. This can be useful for simplifying expressions and solving equations." and "what do I do with exponents when adding" lies in the power of exponents to simplify and manipulate mathematical expressions and equations. It is a fundamental concept that underpins many advanced mathematical operations and has practical applications in various fields.
FAQs about "What Do I Do with Exponents When Adding"
This section provides answers to frequently asked questions about adding terms with exponents.
Question 1: What is the most important thing to remember when adding terms with exponents?
Answer: The most important thing to remember is that the bases of the terms must be the same. If the bases are different, the terms cannot be added.
Question 2: How do I add terms with the same base?
Answer: To add terms with the same base, simply add the exponents and keep the base. For example, x2 + x2 = x4.
Question 3: What if the terms have different exponents?
Answer: If the terms have different exponents, you cannot add them directly. You must first rewrite the terms so that they have the same exponent. For example, x2 + x3 = x2(x1 + x2) = x3 + x5.
Question 4: Can I add terms with different bases?
Answer: No, you cannot add terms with different bases. Terms with different bases must be rewritten using a common base before they can be added.
Question 5: What are some common mistakes to avoid when adding terms with exponents?
Answer: Some common mistakes to avoid include:
- Forgetting to check if the bases are the same- Adding the coefficients instead of the exponents- Not simplifying the expression after adding the exponents
Question 6: Why is it important to understand how to add terms with exponents?
Answer: Understanding how to add terms with exponents is important because it is a fundamental operation in algebra. It is used to simplify expressions, solve equations, and perform other mathematical operations.
Summary: Adding terms with exponents requires careful attention to the bases and exponents of the terms. By following the steps outlined in this FAQ, you can avoid common mistakes and ensure that your answers are correct.
Next Section: Advanced Techniques for Adding Terms with Exponents
Conclusion on "What Do I Do with Exponents When Adding"
In this article, we have explored the topic of adding terms with exponents. We have learned that the key to adding terms with exponents is to ensure that the bases of the terms are the same. Once the bases are the same, we can simply add the exponents and keep the base. We have also learned how to handle terms with different exponents and how to avoid common mistakes.
Understanding how to add terms with exponents is a fundamental skill in algebra. It is used to simplify expressions, solve equations, and perform other mathematical operations. By mastering this skill, you will be well-equipped to tackle more advanced mathematical concepts.
Master Your Medical Exams With PassMedicine
Masterful Witcher 3 Feline Swordsmith Guide
Ultimate Cat Controls Guide: Tame Your Feline Friend
adding and subtracting exponents YouTube

Bedingt Kalligraph Nachdenklich adding with powers 鍔 Ofen Nachlass

the properties of exponents are shown in purple and blue text on white